Bài 1: Tập hợp Q các số hữu tỉ
1. Số hữu tỉ
+ Số hữu tỉ là số: được viết dưới dạng phân số với
+ Tập hợp các số hữu tỉ được kí hiệu là Q
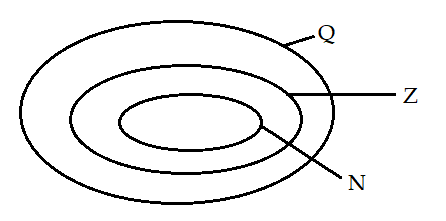
+ Nhận thấy các số nguyên như …; -2; -1; 0; 1; 2; … đều viết được dưới dạng phân số như nên mọi phần tử trong tập số nguyên Z đều thuộc tập số hữu tỉ Q
+ Ta có mối liên hệ giữa tập số tự nhiên, số nguyên và số hữu tỉ như sau:
-> Biếu đồ Ven:
 2. Biểu diễn số hữu tỉ trên trục số
2. Biểu diễn số hữu tỉ trên trục số
+ Đối với số nguyên ta có thể dễ dàng biểu diễn chúng trên trục số
+ Ví dụ để biểu diễn số hữu tỉ trên trục số, ta sẽ làm như sau:
Bước 1: Vẽ trục số, chọn điểm 0 và các các điểm lân cận như 1 hoặc -1
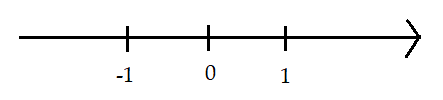
Bước 2: Nhận thấy phân số nên ta sẽ chia đoạn từ điểm 0 đến điểm 1 thành 3 phần bằng nhau, lấy một đoạn làm đơn vị mới.
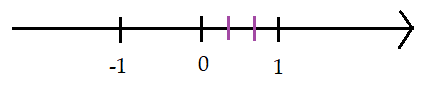
Bước 3: Số hữu tỉ được biểu diễn bởi điểm A nằm bên phải điểm 0 các cách điểm 0 một đoạn bằng 2 lần đơn vị mới
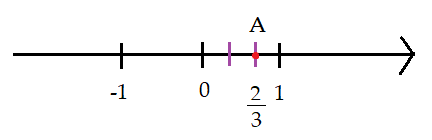
+ Lưu ý: Khi biểu diễn các số hữu tỉ mà có mẫu số âm thì ta phải đổi số hữu tỉ đó dưới dạng phân số có mẫu số dương
3. So sánh hai số hữu tỉ
+ Với hai số hữu tỉ bất kì x, y ta luôn có:
hoặc x = y hoặc x < y hoặc x > y
+ Ta có thể so sánh hai số hữu tỉ bằng cách:
viết chúng dưới dạng phân số cùng mẫu dương rồi so sánh hai phân số đó.
x = ; y =
(m > 0)
So sánh các tử là số nguyên a và b
- Nếu a > b thì x > y
- Nếu a = b thì x=y
- Nếu a < b thì x < y
+ Nếu x < y thì trên trục số, điểm x ở bên trái điểm y
+ Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.
Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.
Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm
Hướng dẫn trả lời lời câu hỏi SGK
?1
Vì sao các số 0,6 ; -1,25; là các số hữu tỉ ?
Hướng dẫn giải:
Các số 0,6; −1,25; −1,25; là các số hữu tỉ vì:
0,6 =
−1,25 =
= 1 +
=
Hay các số 0,6; −1,25; viết được dưới dạng phân số
với a, b ∈Z và b ≠0 nên các số đó là các số hữu tỉ.
?2 Số nguyên a có là số hữu tỉ không? Vì sao?
Hướng dẫn giải:
Số nguyên a luôn viết được dưới dạng (c, d ∈ Z; d ≠0) do đó a là số hữu tỉ.
Ví dụ:
3 = =
=
−2 =
?3 Biểu diễn các số nguyên: -1; 1; 2 trên trục số.
Hướng dẫn giải:
- Số nguyên -1 được biểu diễn bởi điểm A nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 1 đơn vị
- Số nguyên 1 được biểu diễn bởi điểm B nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 1 đơn vị
- Số nguyên 2 được biểu diễn bởi điểm C nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị
Ta biểu diễn trên trục số như sau:

?4
So sánh hai phân số: và
Hướng dẫn giải:
Ta có:
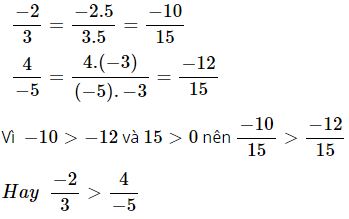
?5 Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm,
số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm ?
;
;
; −4;
;
Hướng dẫn giải:
Số hữu tỉ dương là: ,
Số hữu tỉ âm là: ;
; −4
Số hữu tỉ không là số hữu tỉ dương cũng không là số hữu tỉ âm là:
Hướng dẫn giải bài tập SGK
Bài 1
Điền kí hiệu (∈, ⊂, ∉) thích hợp vào ô vuông
– 3 ... N ; -3 ... Z; -3...Q
-2/3 ... Z; -2/3... Q; N... Z... Q
Lời giải
– 3 ∉ N – 3 ∈ Z -3 ∈ Q
-2/3 ∉ Z -2/3 ∈ Q N ⊂ Z ⊂ Q
Bài 2
Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ
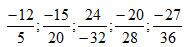
Lời giải
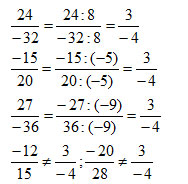
Vậy những phân số biểu diễn số hữu tỉ là:
;
;
Bài 3
So sánh các số hữu tỉ:
a) x = 2/ -7 và y = -3/11
b) x = -213/300 và y = 18/-25
c) x = -0,75 và y = - 3/4
Lời giải
a) x= 2/-7 = -22/7;y = -3/11= -21/77
Vì -22 < -21 và 77> 0 nên x <y
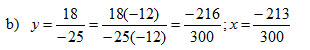
Vì -216 < -213 và 300 > 0 nên y < x
c) x = -0,75 = -75/100 = -3/4; y = -3/4
Vậy x = y
Bài 4
So sánh số hữu tỉ a/b (a,b ∈ Z, b ≠0) với số 0 khi a, b cùng dấu và khi a, b khác dấu
Lời giải
Với a, b ∈ Z, b> 0
Khi a, b cùng dấu thì a/b > 0
Khi a,b khác dấu thì a/b < 0
Tổng quát: Số hữu tỉ a/b (a, b ∈ Z, b ≠0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0
Bài 5
Giả sử x = a/m; y = b/m
(a, b, m ∈ Z, b ≠0) và x < y. Hãy chứng tỏ rằng nếu chọn z = (a+b)/2m thì ta có x < z < y
Lời giải
Theo đề bài ta có x = a/ m; y = b/m (a, b, m ∈ Z, m > 0)
Vì x < y nên ta suy ra a< b
Ta có:
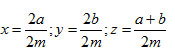
Vì a < b ⇒ a + a < a +b ⇒ 2a < a + b
Do 2a < a +b nên x < z (1)
Vì a < b ⇒ a + b < b + b ⇒ a + b < 2b
Do a+b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z< y